Number System
In Computer architecture, Number System is a technique to represent the numbers in different ways, i.e., we use different symbols and notations. In Computer system, following are the types of Number System:
In Decimal Number System, we have only 10 digits i.e., 0 to 9. That is why the base value or Radix value of Decimal Number System is 10.
2. Binary Number System
In Binary Number System, we have only two symbols of electric pulse - OFF (represents with number 0) and ON (represent with number 1). That is why the base value or Radix value of Binary Number System is 2. Our computer system runs on this Number System, because our computer system works on Digital Signal.
3. Octal Number System
In Octal Number System, we have total 8 numbers i.e., 0 to 7. So, its Base value or Radix value is 8.
Remember, there is also a relationship between Binary Number System and Octal Number System. Because the group of 3 binary digits makes 1 octal digit. Since, 2^3=8.
The representation of all the Octal numbers in Binary form are given below:
4. Hexa Decimal Number System
In Hexa Decimal Number System, we have total 16 numbers. With the Decimal numbers (10) additional 6 numbers are present. These 6 numbers we represent with the English capital alphabets like,
10 - A
11 - B
12 - C
13 - D
14 - E
15 - F
So, its Base value or Radix value is 16 and range is 0 to F (i.e., 15).
Remember, there is also a relationship between Binary Number System and Hexa Number System. Because the group of 4 binary digits makes 1 Hexa digit. Since, 2^4=16.
The representation of all the Hexa Decimal numbers in Binary form are given below:
Conversion rules for converting Decimal Number System to any other number system
Step 1: Identify the target base (i.e., converted base) to which the given decimal number is to be converted.
Step 2: Divide the decimal number by the target base in factorization method till the quotient is coming 0 and write down the each remainder at the beside of the quotient.
Step 3: Identify the first remainder with LSD / LSB and last remainder with MSD / MSB.
Step 4: Arrange all the remainder from MSD to LSD in order to generate the Binary form of the given number.
MSD - Most Significant Digit or MSB - Most Significant Bit
LSD - Least Significant Digit or LSB - Least Significant Bit
 |
| Procedure to convert from Decimal to Binary |
 |
| Procedure to convert from Decimal to Octal |
 |
| Procedure to convert from Decimal to Hexa Decimal |
To know more about conversion from Decimal to any other number system, please follow the video:
Conversion rules for converting any number system to Decimal Number System
Step 1: Identify the base value of the given number, which you want to convert into decimal.
Step 2: Then assign the position of each digit of the number from right to left direction from the position value 0.
Step 3: Multiply the digit into the base of position power. (i.e., using the following formula)
 |
| Procedure to convert from Binary to Decimal |
 |
| Procedure to convert from Octal to Decimal |
 |
| Procedure to convert from Hexa Decimal to Decimal |
To know more about conversion from any other number system to Decimal, please follow the video:
Author
Hi, Its me Hafeez. A webdesigner, blogspot developer and UI/UX Designer. I am a certified Themeforest top Author and Front-End Developer. I'am business speaker, marketer, Blogger and Javascript Programmer.
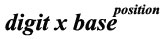
0 Comments:
Post a Comment